問371との公約数を答えなさい。 問427と53の最大公約数を答えなさい。 問521と24の公倍数を答えなさい。 問621と26の最小公倍数を答えなさい。 問、の最小公約数を答えなさい。 問7の最大公倍数を答えなさい。By 最大 公約数 問題 難しい キーを指定することにより、12通りのキーに移調して楽譜を出力することができます。 どんな楽器にでも対応できる楽譜が容易に手に入ります。 こんばんは。 Twitterのトレンドを見ていて、日本は平和だなーと思いました(白目)。 今日は「よく聞く『最大公約数的な~』はベン図を使うと分かりやすいよ」というお話です。 これでインテリ層がよく使う「最大公約数」の理解は間違いなし!
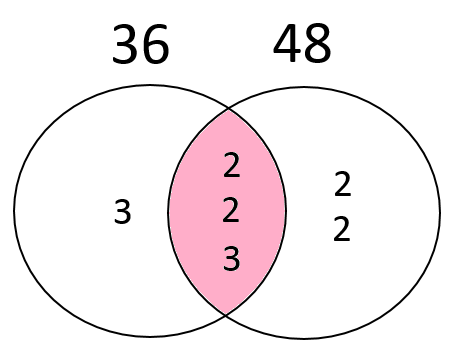
小学算数 最大公約数と最小公倍数を図を使って理解する 偏差値40プログラマー
最大公約数 問題 難しい
最大公約数 問題 難しい-問題の計算量 その問題を解くアルゴリズムの計算量の下限 最も効率良く解くと、どれ位で解けるか = どうしてもどれ位必要か = どれ位難しい問題か ¡! 最小公倍数 公約数・最大公約数の動画です。 なぜ、最大公倍数はなく最小公倍数になるのか、最小公約数ではなく最大公約数になるのかについても考えてください。 最大公約数と最小公倍数の応用問題




どちゃ楽数学bot A Twitter 解答です 1 とても難しいです 最大公約数とったらなんか行けました とおもいます 最大公約数 を取ってくると互いに素を利用して扱いやすくなる問題はたまにあります 2 最初はちょっとヤバそうって感じますが 分かるとなんか そうね っ
最大公約数 を求める1つの方法は,共通な数で割れるだけ割っていく方法です. このとき,共通に割れる数の積が最大公約数です. 最小公倍数 を求める方法は,これと同様ですが,割った数と残った数を掛けます. 例 次の例で, 12 , 18 の最大公約数は 6 公約数は、すべて最大公約数の約数になっています。よって、最大公約数が分かれば、公約数はすべて分かります。また、 a と b の最大公約数が 1 のとき、 a と b は 互いに素 であると言います。 公約数を文字で置く 整数の性質から文字で置く練習をして そもそもユークリッドの互除法とは 二つの最大公約数を求めるアルゴリズム です 二つの整数の大きい方から小さい方を引くことを二つの整数が等しくなるまで繰り返す 等しくなった値が最大公約数 ではまずなぜそうなるのかを考えましょう 100 と 25 の
問題の見通し力をつけるには、文字で置かずとも、どこが最大公約数を作っているのかという2数の関係が見えるようになることが重要です。 案の定、この生徒は (2) で (1) を活かしきれず、遠回りな解答を作ってしまっていました。ある2つの数の最大公約数を求めるとき、これまではそれぞれの数を素因数分解して求めてきたね。でも、例えば 「722と171の最大公約数は?」 などのように 大きい数の最大公約数 をたずねられると、それぞれの数を素因数分解するのはちょっと骨が折れそうだ。 意見の最大公約数で結論づけても何も生まれ 参加者の思考の差異により、一つの方向に決めることが難しい 誰も責任を持つことなく、その場にいるあらゆるメンバーの異なるポリシーや意見の最大公約数が反映され、本質的な問題
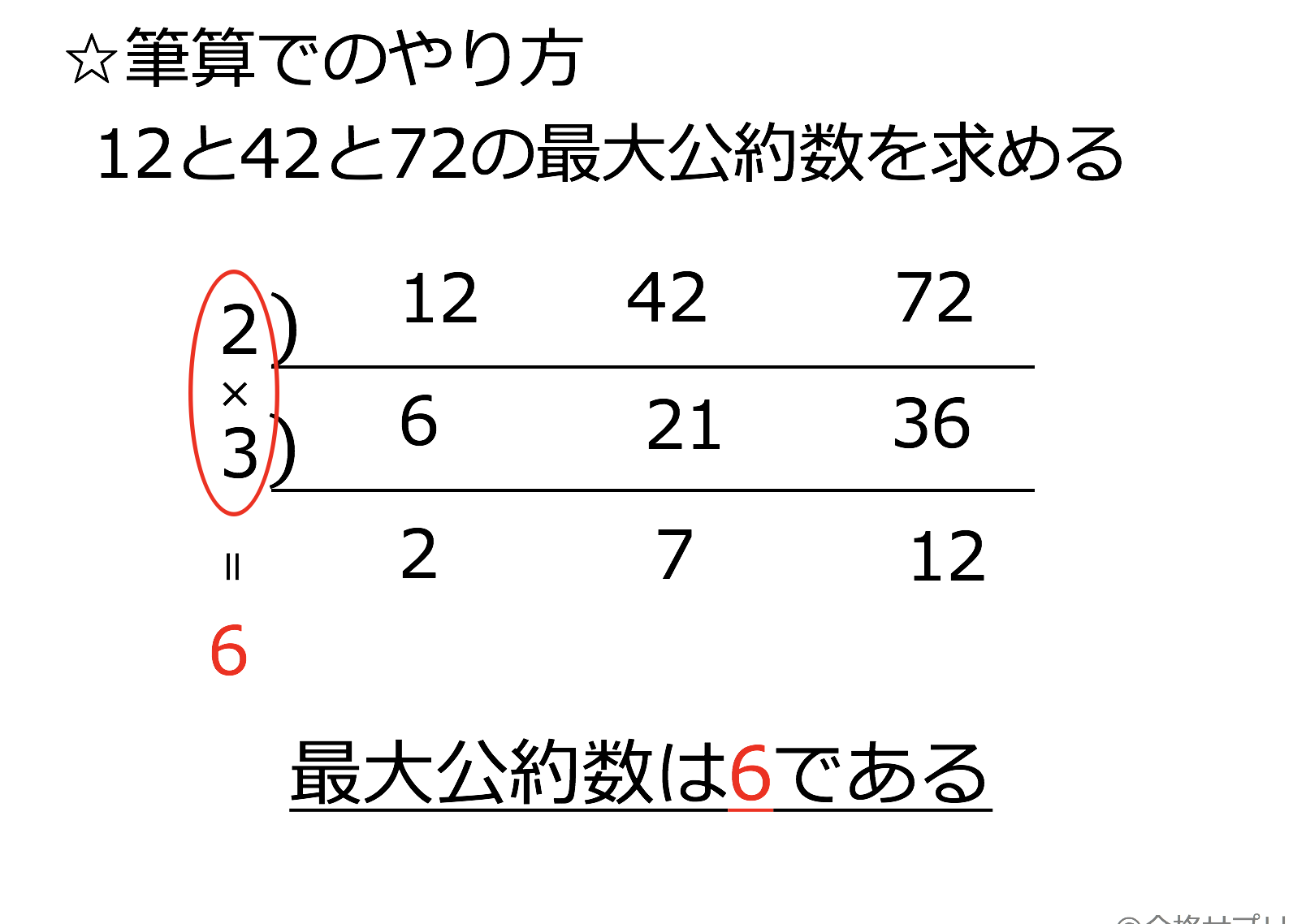
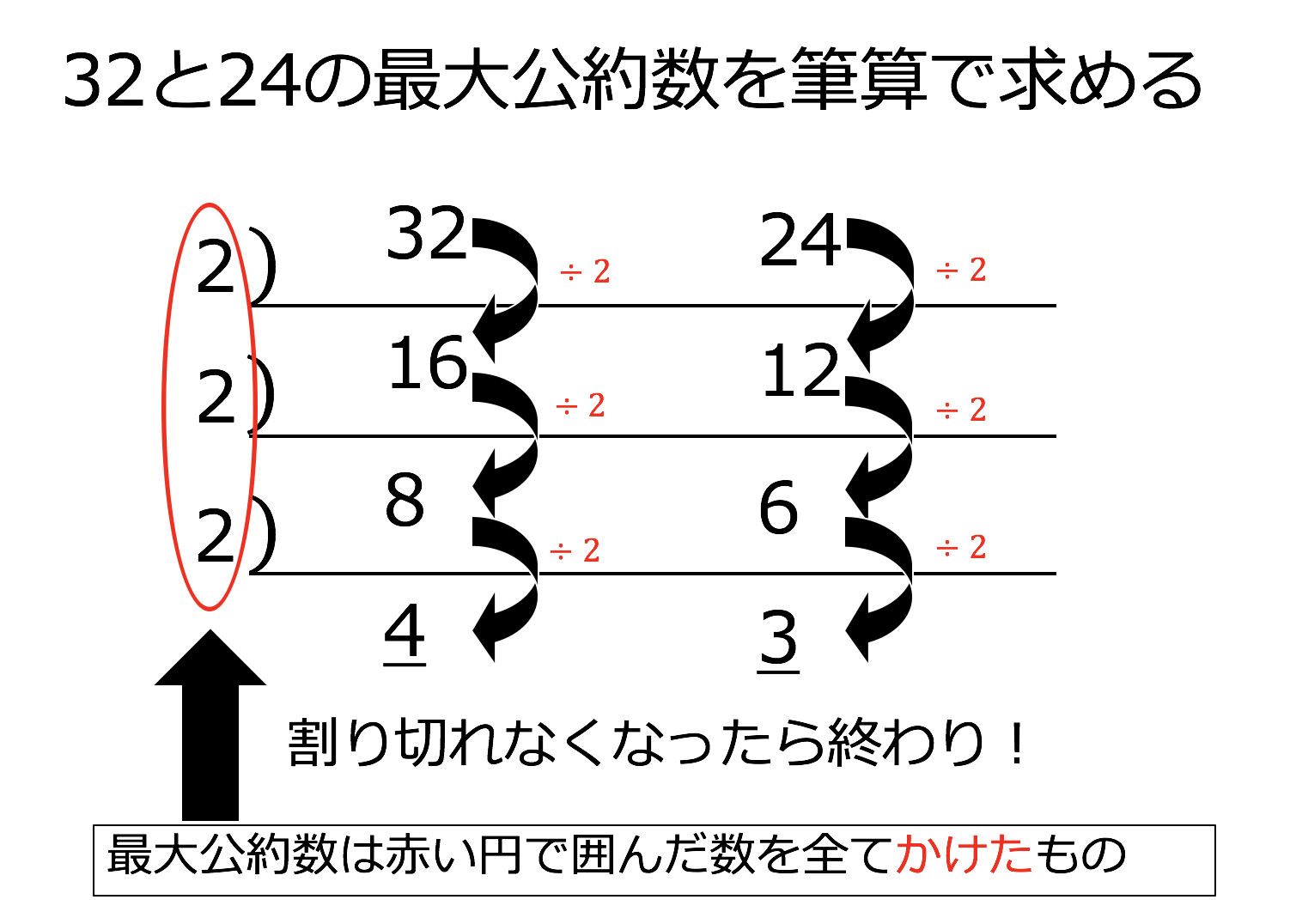
2数が互いに素となったら、割った数を全て掛け合わせた答えが最大公約数 となります。 よって18と24の最大公約数は2×3=6です。 また互いに素となった2数も合わせて掛ければ、最小公倍数を求めることができます。1 最大公約数 問題 2 つの整数a,b の最大公約数を求める(ただしa2 最大公約数の求め方 最大公約数の求め方を復習す る。 ・約数をすべて並べて求める。 ・素因数分解を用いて求める。 ・ユークリッドの互除法を用い て求める。 最大公約数の最適な解法 〇それぞれの解法のよさを認識 する。 ・交流活動を行う。



最大公約数の意味と求め方 センター試験で使える解法を紹介 Studyplus スタディプラス




最大公約数の問題はこれで完璧 約数を漏れなく求める方法と公約数の見つけ方
92.最大公約数の求め方 *問題文の一部訂正 計算していると答は分かるのです が、解答として分かりやすく書くとなると、なかなか難しい。結局しらみつぶしのよ うなことになってしまいました。 公約数と公倍数の自主学習ノート例 15年3月3日 年5月4日 公約数と公倍数の練習問題を解いてみましょう。 分数の計算をするために必要ですので、考え方をよく理解した後は、たくさん練習をして、速く正確に答えられるようにしていきたいですね中学受験の算数・理科ヘクトパスカルによる「最大公約数と最小公倍数の問題」の手書き解説です。 ある整数Aと72の最大公約数は12です。これについて,次の問いにこたえなさい。 (1) この2つの整数の最小公倍数が360であるとき,Aはいくつですか。



Fdk3a7ctb5192box5b Com Es 5nen Mt Yakusu Html



約数 倍数の問題です どうか教えてください 8と の最大公約 Yahoo 知恵袋
・公約数・最大公約数を工夫して求める。 ・公約数を利用して,問題を解決する。(本時) ・まとめをする。 4本時の学習指導 学 習 活 動 問題を解決していく課程 教 師 の 支 援 と 評 価 1 本時の課題をしり, 問題をよむ。 ・ワークシートに直線をかき ③一番最初に割り切れた数が、二つの数の最大公約数→12と18の最大公約数は6 小6以上ならぜひ解けてほしいところですね(笑) では、第2問! 1113と3763の最大公約数を求めてください。 制限時間は3分です! ————— ———— ——— —— — さて、どう問題集 問題数・問題構成etc 数学Ⅰ・Aは、整数、図形、確率など難易度の高い分野が並んでいる。 この手の分野は、標準問題といえど、比較的難しい問題が多い。 しかし、裏を返せば実力UP! 程度の問題がスラスラ解けるようになれば、難関大で合格点



最小公倍数とは 求め方や計算問題 最大公約数との関係 受験辞典




最大公約数を求める練習問題 計算ドリル 問題集 数学fun
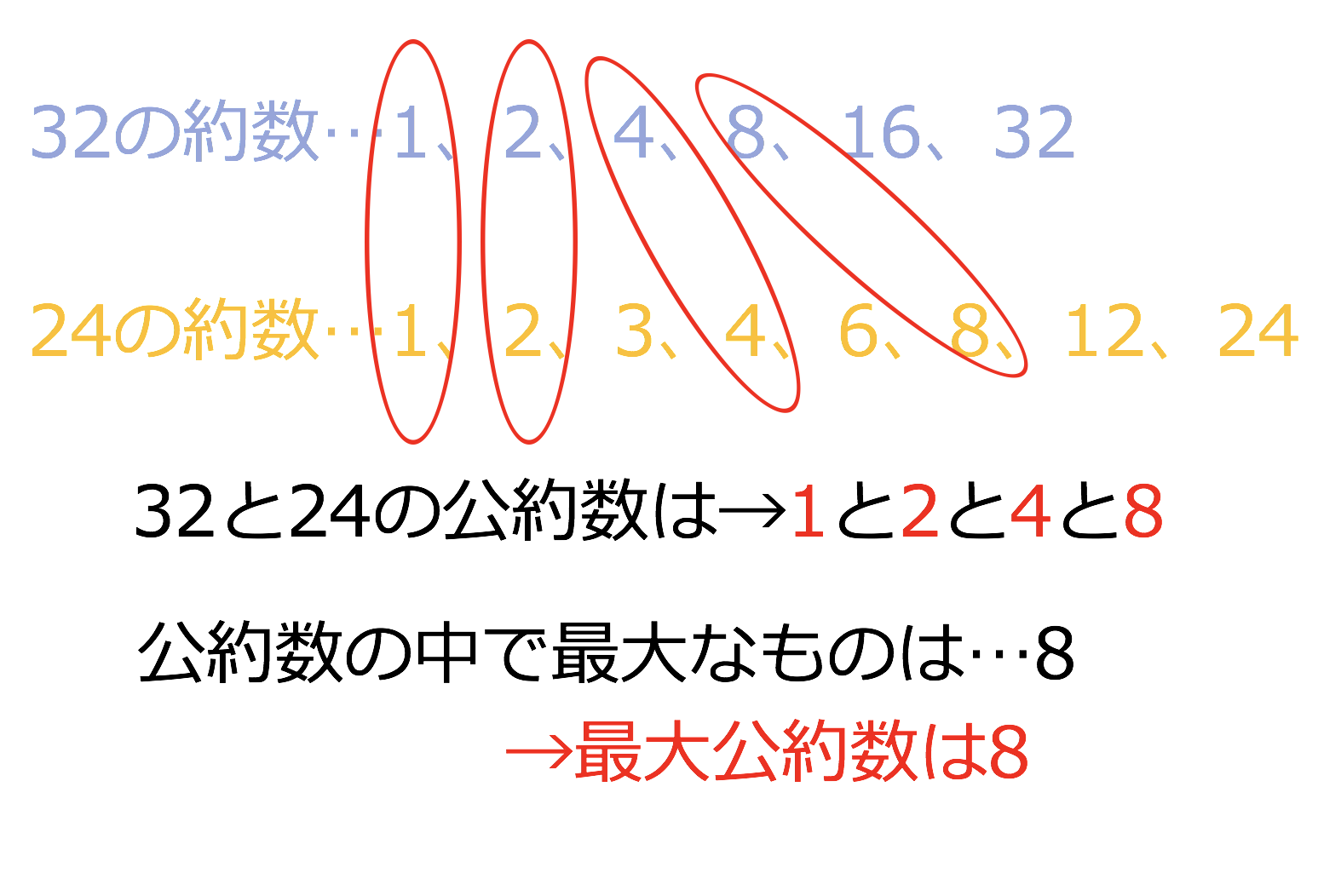
なかなか難しいですよね・ 最大公約数・最小公倍数 問題 2つの整数a、bがあります。aとbの最大公約数は10、最小公倍数 1です。aがbより大きい整数のとき、a、bの数の組みあわせをすべて求めな さ次 演習問題 上 整数の約数と倍数 前 約数・倍数と最大公約数 ユークリッドの互除法 24と42の最大公約数を求めようとすれば,いずれをも割り切る素数を見い出して, 順に割っていくのだ.学習する学年:小学生 1.最大公約数の説明 最大公約数とは、2つ以上の正の整数(自然数)に共通な約数のうち最大の数のことをいいます。但しゼロは除きます。 つまり、公約数の中で一番大きな共通する数が最大公約数ということです。 みなさんは、約数の意味と求め方は覚えていますか?
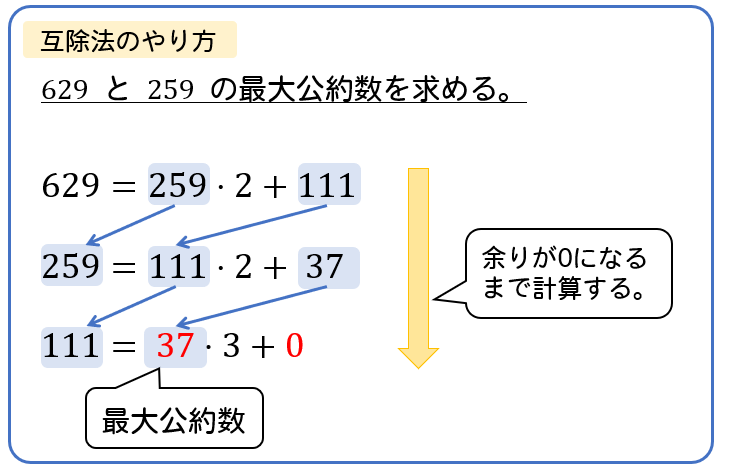



ユークリッド互除法のやり方 最大公約数を求める手順をイチから解説 数スタ



最大公約数と最小公倍数
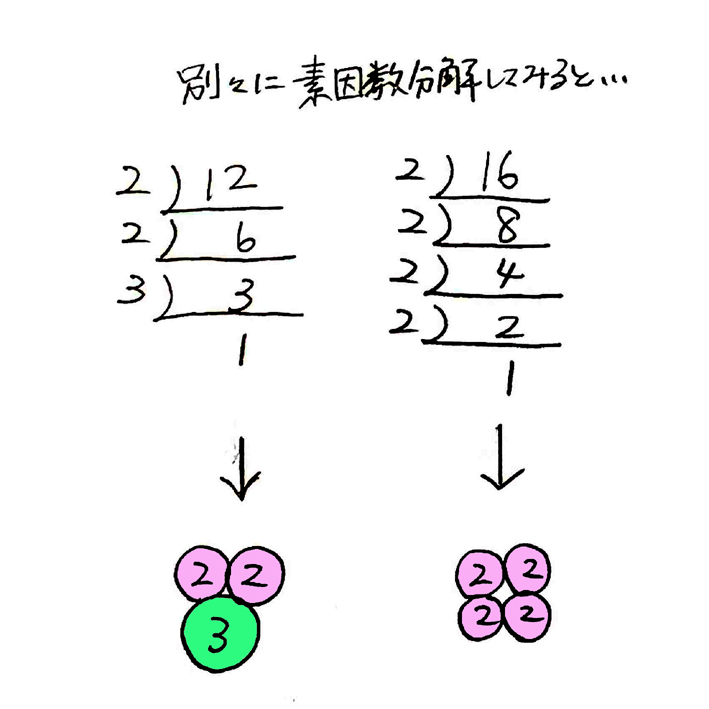
スライド 3 目次 iアルゴリズムの世界 スライド 6 アルゴリズム例:10進数から2進数への変換 10進数と2進数 スライド 9 スライド 10 の分類 素数発見問題は難しい アルゴリズム論で np 問題 (計算機科学最大の問題最大公約数を求める 単純なアルゴリズムの時間計算量 (1) b = 1, 2, , a 0 に対し,a 0 と a 1 の公約数か否か をチェック (2) 最大の公約数を出力 合計ステップ数= 入力サイズ log 2 a 0 に関して指数時間のアルゴリズム 「数の入門と算数 」シリーズは今回で 完結 です。 最終回 のテーマは「 素因数分解 , 約数の個数と総和 , 公約数と公倍数 」です。 前々回( 約数と倍数 素数と素因数分解 ) 、 前回( 指数のしくみ 約分と素因数分解 ) 、と続いてきた「 素因数分解 3 部作 」の 完結編 になります。
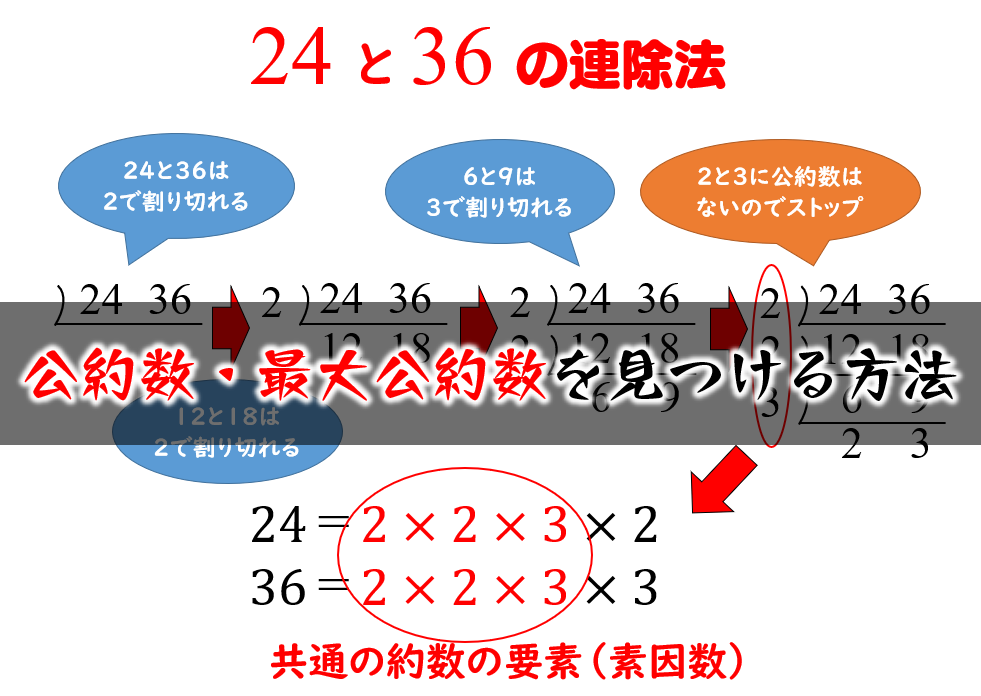



公約数 最大公約数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun



3
学習院大入試問題 数学大問別出題分野 理系らしく微分法・積分法(数Ⅲ)からの出題が多いが、比較的幅広い分野からも出題される。 特に、場合の数と確率からの出題と、図形的考察をともない計算が煩雑な問題は頻出である。 標準難度の設問が多い最大 公約数 問題 難しい by 仮面ライダーゴースト 全 話 仮面ライダーゴースト 全 話 最大公約数に関連する問題は、主に2パターンしかありません。 一つ目は「ユークリッドの互除法」を利用するパターン。 もう一つは、最大公約数をg、最小公倍数をlを置き、4式1条件を作るパターンです。 具体的には、aとbの2整数に対して
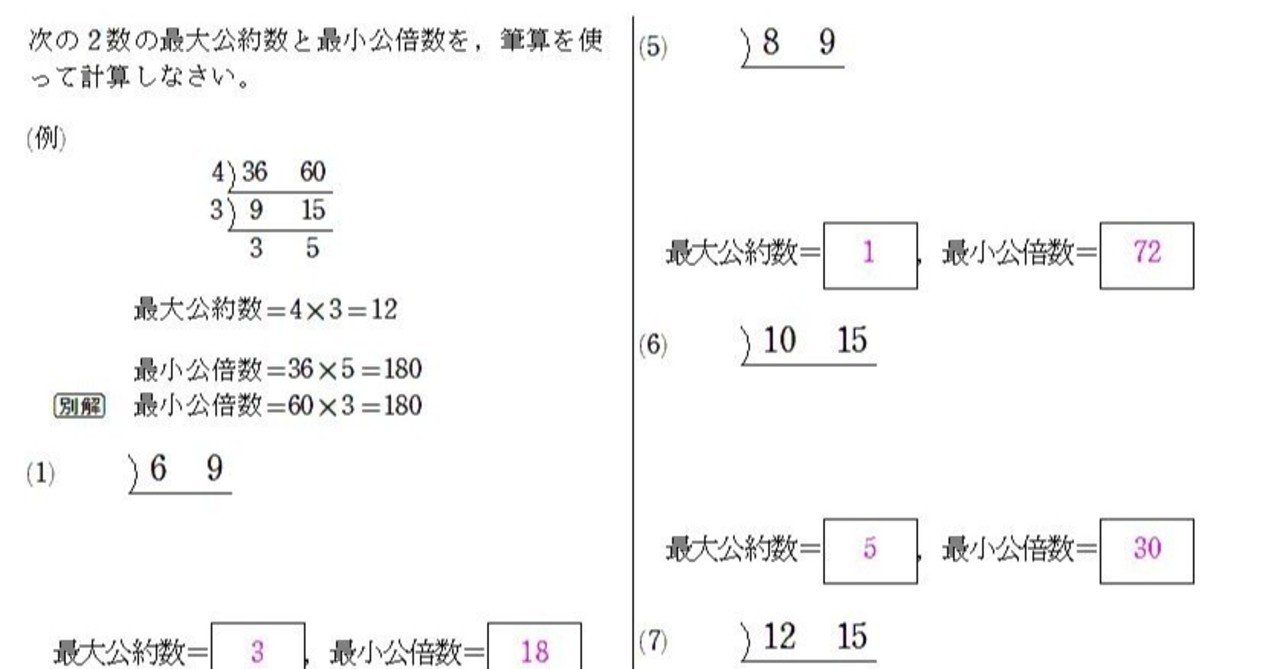



算数基礎ドリル 最大公約数と最小公倍数の筆算 Numachi Note
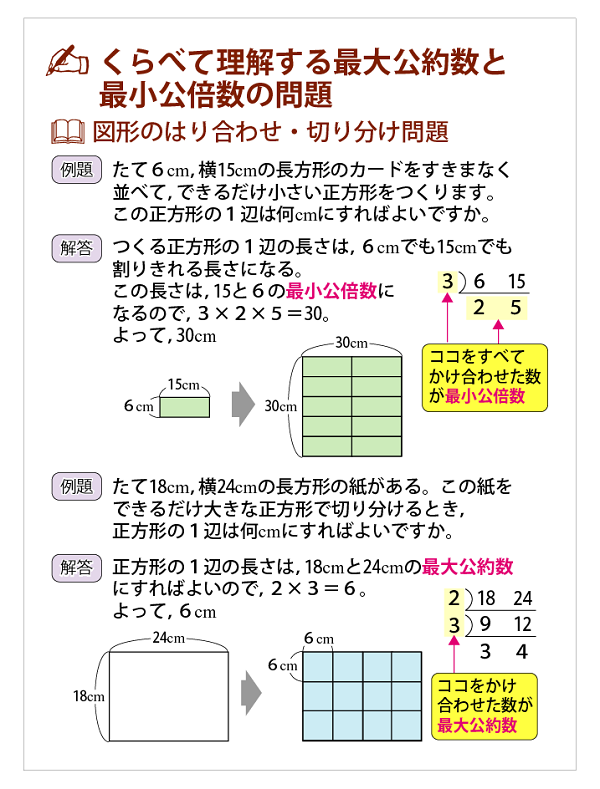



くらべて理解する最大公約数 最小公倍数の問題 恋する中高一貫校 適性検査 徹底攻略
最大公約数を求める方法と聞かれてあなたは何と答えますか? 割り算を逆に書いて、小さい数からどんどん割っていくというのが真っ先に思い浮かぶと思います。 それでは、3355と2379の最大公約数を求めてみましょう。 このように大きい数の最大公約数を求めるとき、2でも割れない、3でも、52W数学演習V・VI 標準M1053 担当教員 宮地兵衛 研究室 33 Emailmiyachi@mathnagoyauacjp ユークリッドの互除法 ここでは0 でない2 つの多項式f(x), g(x) の最大公約式を具体的に求める方法として, ユークリッドの互除法について説明する①と全く同じ問題なんですけれどね 122-14=108を割り切れる つまり、108の約数 86-14=72を割り切れる つまり、72の約数 したがって 108と72の公約数だから 最大公約数36の約数 そして 14余るから、14よりも大きい数




Newみんなの算数講座38 マジョリティーとマイノリティー 中学受験の算数知恵宝庫




倍数と約数 最大公約数を求める 練習問題 Youtube
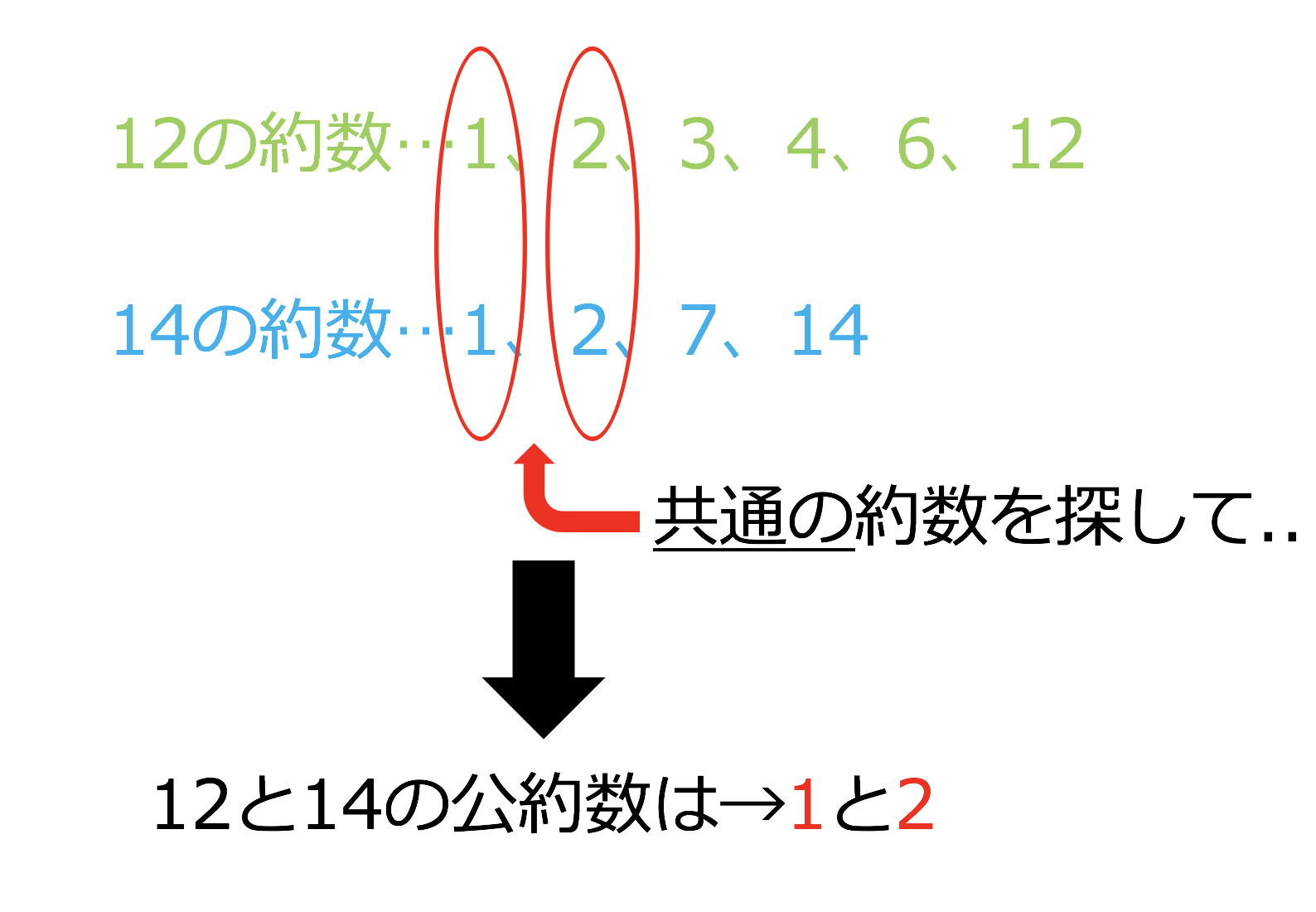
10と12の公約数は、1、2となります。 そして、このとき最大の約数を 最大公約数 といいます。 今回の場合は、 2 ですね! それでは、問題です。 次の数の最大公約数と公約数を求めよ。 例題① 6と12 例題② 14と21 例題③ 51と68 例題③はちょっと難しいです 1つ難しいポイントをあげるならば、 置き換え です。 A,Bという2つの数字の最小公倍数を求める際に、gをA,Bの最大公約数として、A = gA′ A = g A ′ 、B = gB′ B = g B ′ とおき、最小公倍数はgA′B′ g A ′ B ′ とするやつです。 たとえば、「積が2700、最小公こんにちは 最大公約数と最小公倍数の問題です。 難しいと思いますが、分かる方いらっしゃいましたら説明お願いします🙇♀️🙇♀️ 3つの自然数 40, 56, n の最大公約数が8,最小公倍数が1400 であるとき, nをすべて求めよ。 40= 225 56=27 3 0F 8= 2 (400
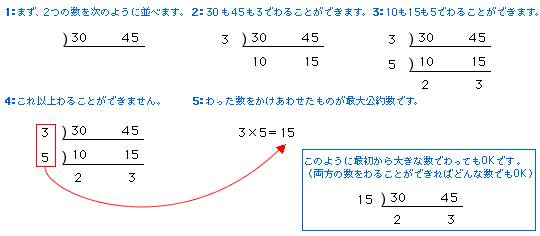



約数 公約数 最大公約数 算数の教え上手 学びの場 Com




どちゃ楽数学bot A Twitter 解答です 1 とても難しいです 最大公約数とったらなんか行けました とおもいます 最大公約数 を取ってくると互いに素を利用して扱いやすくなる問題はたまにあります 2 最初はちょっとヤバそうって感じますが 分かるとなんか そうね っ
17年 東大文系数学 第4問 理系数学 第4問 (ユークリッドの互除法・漸化式・対称式・最大公約数)17年は、整数問題が文理共通でした。 簡単だ、簡単だと言われ続けている今年の数学ですが、これは難しかったと評判です。最大公約数だから、4式1条件を作ろう では、難しそうな奇数の場合。 と言っても、実は基礎の積み重ねで解くことができます。 というのも奇数の場合は最大公約数が2となりますが、 先ほども書いた通り最大公約数と言われたら、 ①ユークリッドの互除法




青チャートの整数の問題です Clear



最小公倍数とは 求め方や計算問題 最大公約数との関係 受験辞典




どちゃ楽数学bot A Twitter 解答です 1 とても難しいです 最大公約数とったらなんか行けました とおもいます 最大公約数 を取ってくると互いに素を利用して扱いやすくなる問題はたまにあります 2 最初はちょっとヤバそうって感じますが 分かるとなんか そうね っ




小学算数 最大公約数と最小公倍数を図を使って理解する 偏差値40プログラマー
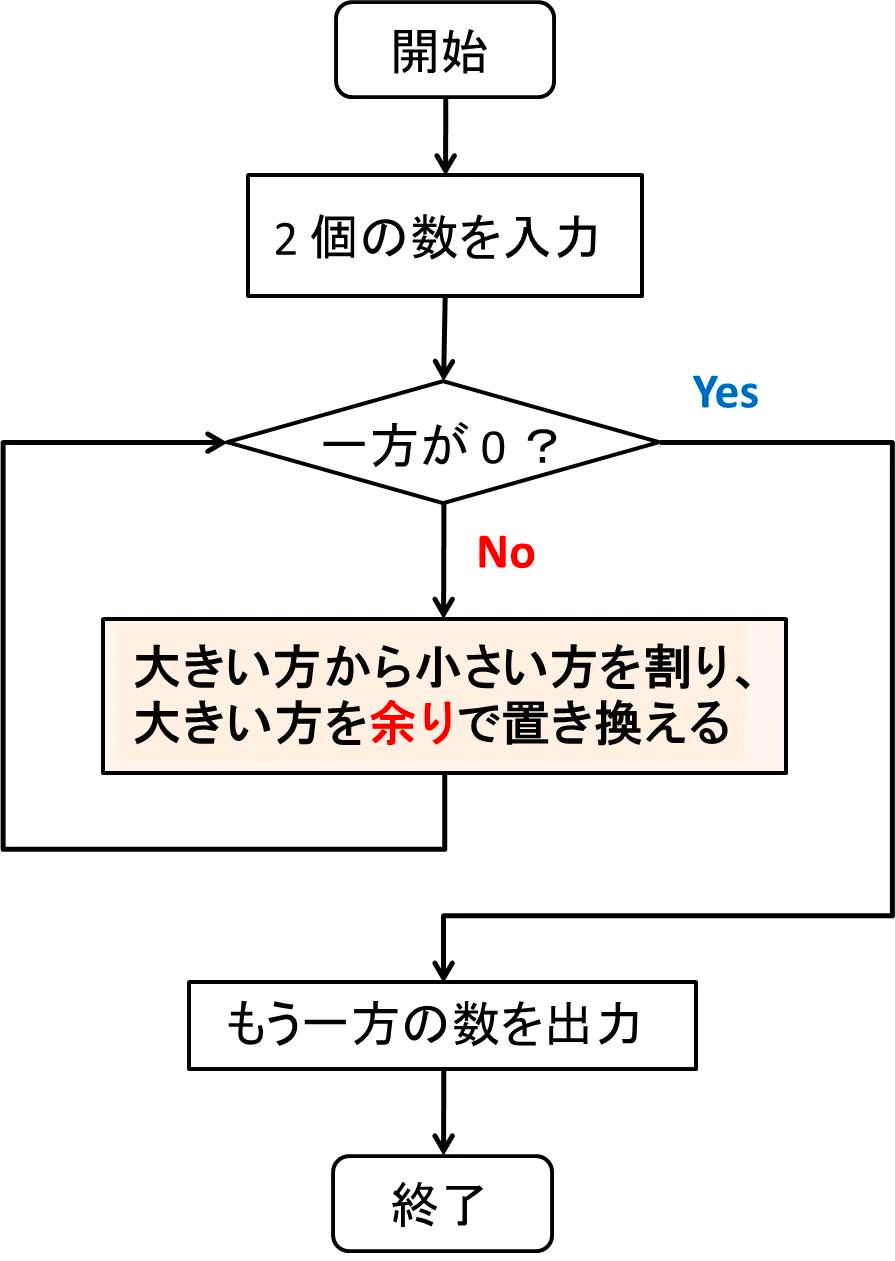



Atcoder 版 マスター オブ 整数 最大公約数編 Qiita




3分で分かる 最大公約数の意味 3通りの求め方をわかりやすく 合格サプリ




最高の公倍数 公約 数 子供のための最高のぬりえ




最大公約数と最小公倍数の問題です 難しいと思いますが 分かる方いらっしゃいましたら説 Clear




3分で分かる 最大公約数の意味 3通りの求め方をわかりやすく 合格サプリ




最大公約数と最小公倍数の求め方とは ヒント 素因数分解 遊ぶ数学




小5 算数 小5 倍数 約数の文章題 Youtube




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




公約数 公倍数の求め方 Z Square Z会




最大公約数レベル2 問題 296 400
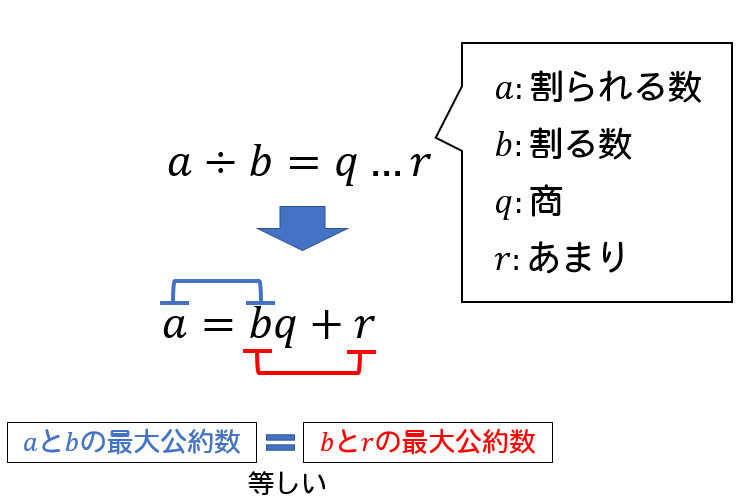



ユークリッド互除法のやり方 最大公約数を求める手順をイチから解説 数スタ




サイコロと最小公倍数 最大公約数 年 北海道大 理系 数学日和




公倍数 最小公倍数の簡単な見つけ方 連除法を使う方法と使わない方法 数学fun 最小公倍数 小学校 算数 数学



3分で分かる 最大公約数の意味 3通りの求め方をわかりやすく 合格サプリ




2018年 東大理系数学 第2問の解説 数列 互いに素 最大公約数 理系と文系 オンライン受講 東大に 完全 特化 東大合格 敬天塾




どちゃ楽数学bot 解答です 1 とても難しいです 最大公約数とったらなんか行けました とおもいます 最大公約数 を取ってくると互いに素を利用して扱いやすくなる問題はたまにあります 2 最初はちょっとヤバそうって感じますが 分かるとなんか そうね




最大公約数と最小公倍数の意味 これをタイルでイメージ出来ますか 七田式天六教室 本町教室及び魔法の折り紙オンライン教室は算数 数学のスペシャリストを育てます
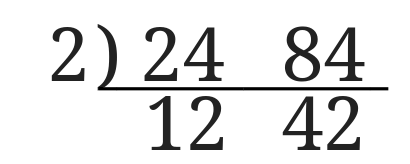



連除法 はしご算 を使った最大公約数の求め方と求められる理由とは まぜこぜ情報局



3



3分で分かる 最大公約数の意味 3通りの求め方をわかりやすく 合格サプリ




小学校算数 中学受験 最大公約数と最小公倍数 解説 Youtube




サイコロと最小公倍数 最大公約数 年 北海道大 理系 数学日和




Excel Gcd Lcm関数 最大公約数 最小公倍数を求めたい くうねるのエクセル教科書




算数の公約数 最大公約数を完全解説 簡単な求め方や計算方法 センター試験対策も紹介 学びtimes



覚えておきたい最小公倍数と最大公約数の求め方 盛り上がれ秋田



最小公倍数 最大公約数のドリル




図で理解する ユークリッドの互除法 大学入試数学の考え方と解法




最大公約数 Instagram Posts Gramho Com




3分で分かる 最大公約数の意味 3通りの求め方をわかりやすく 合格サプリ




公約数 最大公約数の簡単な求め方 算数パラダイス



最小公倍数の求め方や性質を全て解説 実際の入試問題の解説付き Studyplus スタディプラス



最小公倍数の求め方や性質を全て解説 実際の入試問題の解説付き Studyplus スタディプラス




最大公約数 最小公倍数 小学生




開成高校 整数問題 最大公約数 最小公倍数 Youtube



2つの整数の最大公約数 最小公倍数と 3つの整数の最大公 Yahoo 知恵袋




横浜の名門校 聖光学院 はレゴで真理を学ぶ 名門校の不思議な授業 東洋経済オンライン 社会をよくする経済ニュース




3分で分かる 最大公約数の意味 3通りの求め方をわかりやすく 合格サプリ




最大公約数と最小公倍数の求め方とは ヒント 素因数分解 遊ぶ数学




2019年東大数学理系第4問 整数 最大公約数 ユークリッドの互除法 オンライン受講 東大に 完全 特化 東大合格 敬天塾




最高の公倍数 公約 数 子供のための最高のぬりえ




コがわからないです なぜ最大公約数 最小公倍数を素因数分解するのか Clear



最大公約数の意味と求め方 センター試験で使える解法を紹介 Studyplus スタディプラス



3分で分かる 最大公約数の意味 3通りの求め方をわかりやすく 合格サプリ
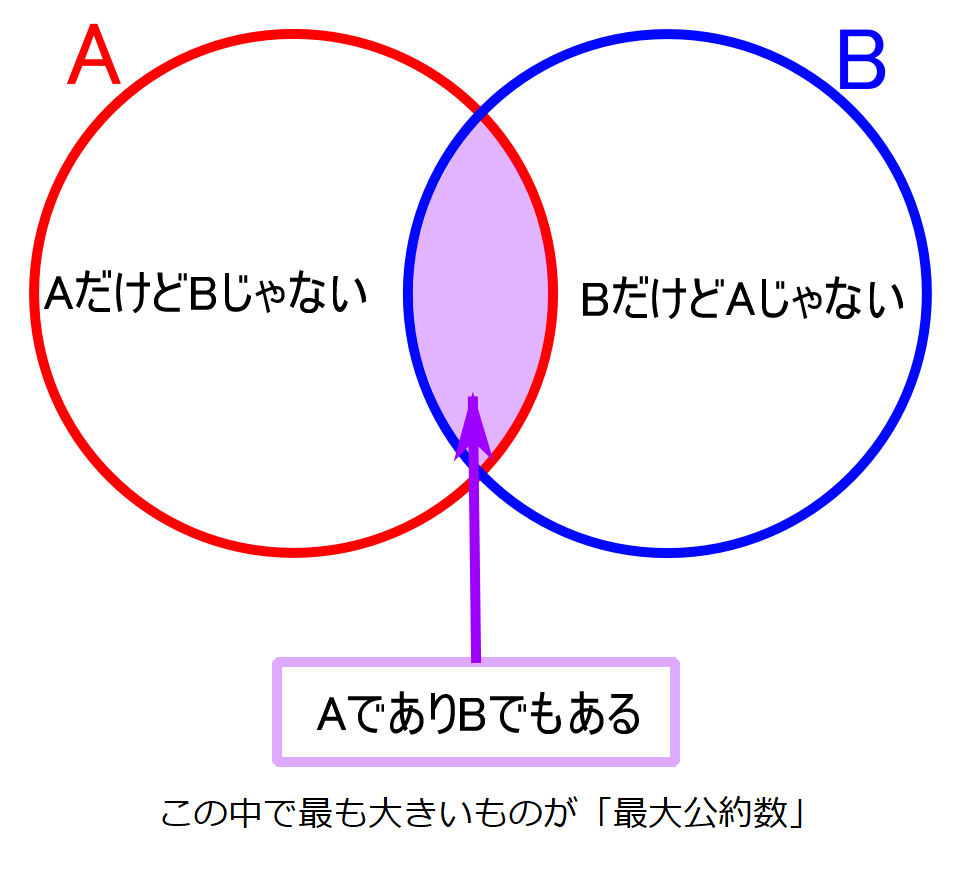



よく聞く 最大公約数的な はベン図を使うと分かりやすいよ あっきー Note



算数に詳しい人教えて下さい 68と85の最大公約数は17らしいのですが Yahoo 知恵袋




小学5年生 算数 8月 約数と公約数 公倍数 公約数の利用 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




算数基礎ドリル 最大公約数と最小公倍数の筆算 Numachi Note



北海道大学 理系 数学入試問題 Cccpcamera Blog




第1回 Pythonで最大公約数と最小公倍数のプログラムを書いた 疑念は探究の動機であり 探究の唯一の目的は信念の確定である



48s96ub7b0z5f Net Saidaikouyakusuu Saisyoukoubaisuu




最小公倍数と最大公約数の問題をユークリッド互除法で解決 また 倍数の証明も解説 数学ia Himokuri




整式とは 整式の最大公約数と最小公倍数の求め方




2017年 東大文系数学 第4問 理系数学 第4問 ユークリッドの互除法 漸化式 対称式 最大公約数 オンライン受講 東大に 完全 特化 東大合格 敬天塾




高校数学 ユークリッドの互除法でなぜ最大公約数が求められるのか ゼロから稼ぐブログ生活
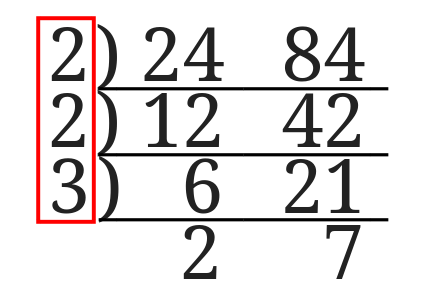



連除法 はしご算 を使った最大公約数の求め方と求められる理由とは まぜこぜ情報局




14年10月 怜悧玲瓏 高校数学を天空から俯瞰する



最小公倍数と最大公約数の意味 Colorfultube
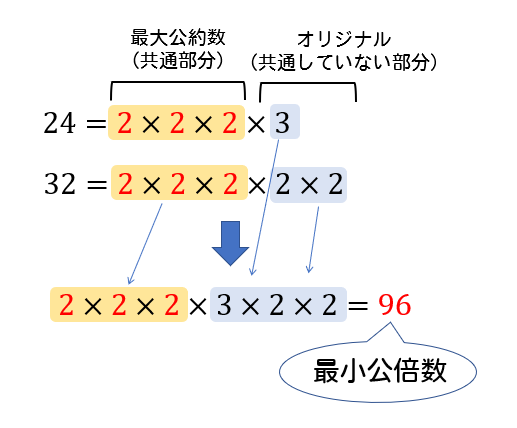



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




最大公約数と最小公倍数の暗記ドリル たぶお Sapix サピックス A1 養成講座




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ



1



中学受験の問題です 最小公倍数 最大公約数に関する添付の問題なの Yahoo 知恵袋




大きな数の最大公約数の求め方 Youtube




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ



3つの自然数abc A B C について Aとbとcの最大公約数は12 Yahoo 知恵袋




第回 数の性質 約数と倍数 分数 6年生 日能研の歩き方



Fdk3a7ctb5192box5b Com Es 5nen Mt Baisu Html




最高の公倍数 公約 数 子供のための最高のぬりえ



3




公約数 最大公約数の簡単な求め方 算数パラダイス
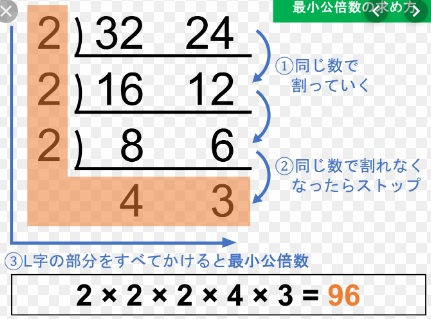



最小公倍数の求め方はすだれ算 小学生向け 塾なしで中学受験



最高の公倍数 公約 数 子供のための最高のぬりえ



3分で分かる 最大公約数の意味 3通りの求め方をわかりやすく 合格サプリ



最小公倍数とは 求め方や計算問題 最大公約数との関係 受験辞典



この指針のa Bp Qの部分の Aとbの最大公約数と Bとrの最 Yahoo 知恵袋



算数 日本語 Colorfultube



最大公約数の意味と求め方 センター試験で使える解法を紹介 Studyplus スタディプラス



最大公約数の意味と求め方 センター試験で使える解法を紹介 Studyplus スタディプラス




小学5年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生




公約数 公倍数の求め方 Z Square Z会



5年生分数のたし算とひき算 倍数 約数 通分 約分の指導 教材 算数5年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




5年生 小学生向け手作り問題集 パパしゅく



小学校6年生の算数の問題です 24とある整数の最大公約数は6 最小公倍 Yahoo 知恵袋



最小公倍数とは 求め方や計算問題 最大公約数との関係 受験辞典



0 件のコメント:
コメントを投稿